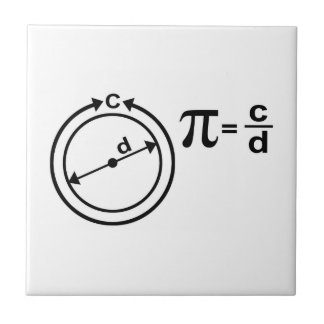
Pi
Pi, usually written \(π\), is a number equal to the ratio of a circle’s circumference to its diameter. The value of \(π\) is approximately \(3.141593\).
If the length of a curve seems like an ill-defined concept to you (maybe you only understand how lines could have lengths), consider bigger and bigger regular polygons that make better and better approximations of the circle. As the number of sides \(N\) of the polygon goes to \(∞\), the perimeter will approach a length of \(π\) times the diameter.
One could also define \(π\) to be the area of a circle divided the area of a square, whose edge is the radius of the circle.
What Kind of Number It Is
It’s not an Integer.
If the diameter here is 1, then the perimeter of the hexagon is 3, the perimeter of the square is 4, and the circumference of the circle is in between. There are no integers between 3 and 4.
It’s not rational, nor is it algebraic. It’s transcendental.
Children:
- Pi is irrational
The number pi is famously not rational, in spite of joking attempts at legislation to fix its value at 3 or 22⁄7.
Parents:
- Mathematics
Mathematics is the study of numbers and other ideal objects that can be described by axioms.